اجعل بياناتك تتحرك: إنشاء رسوم متحركة بلغة بايثون للعلوم والتعلم الآلي

بصفتي عالم بيانات وأستاذاً جامعياً، غالباً ما أحتاج إلى شرح آليات عمل خوارزميات التعلم والمفاهيم الرياضية، سواء في العروض التقديمية التقنية أو المحاضرات الصفية أو المقالات المكتوبة. في كثير من الحالات، يمكن للرسوم البيانية الثابتة أن تُظهر النتيجة النهائية، لكنها غالباً ما تعجز عن توضيح العملية الكامنة وراءها.

في هذا السياق، يمكن للرسوم المتحركة أن تُحدث فرقاً كبيراً. فمن خلال عرض سلسلة من الإطارات، يُظهر كل منها مخططاً يُمثل خطوة في العملية، يُمكنك جذب انتباه جمهورك بشكل أفضل وشرح المفاهيم المعقدة وسير العمل بفعالية أكبر.

ستوضح لك هذه الدورة التدريبية كيفية استخدام لغة بايثون ومكتبة Matplotlib لتحويل الأفكار العلمية إلى واقع ملموس من خلال الرسوم المتحركة. سواء كنت عالم بيانات تُصوّر خوارزمية تعلم آلي، أو مدرس فيزياء يُوضّح الحركة التوافقية، أو كاتبًا تقنيًا تسعى إلى تبسيط الرياضيات، فهذا الدليل مُصمّم خصيصًا لك.

إعداد الرسوم المتحركة الأساسية باستخدام Matplotlib

لنبدأ بتعريف فئة FuncAnimation من حزمة Animation في مكتبة Matplotlib من خلال تحريك دالة الجيب. يمكن تكرار الخطوات التالية في جميع الحالات تقريبًا.

• استورد المكتبات المطلوبة

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

FuncAnimation من matplotlib.animation هي الفئة التي تسمح لك بإنشاء الرسوم المتحركة عن طريق استدعاء دالة التحديث بشكل متكرر.

• تحديد البيانات المرسومة (دالة الجيب)

x = np.linspace(0, 2 * np.pi, 1000)
y = np.sin(x)

تحسب المعادلة y = np.sin(x) جيب كل قيمة من قيم x. هذه هي الموجة الجيبية الأولية التي سيتم رسمها.

• إنشاء المخطط الأولي

fig, ax = plt.subplots()
line, = ax.plot(x, y)
ax.set_ylim(-1.5, 1.5)

تقوم الدالة line, = ax.plot(x, y) برسم الموجة الجيبية الأولية وتخزين كائن الخط في line.

ملاحظة: الفاصلة بعد السطر مهمة: فهي تفكك المجموعة المكونة من عنصر واحد والتي تم إرجاعها بواسطة plot.

• تحديد دالة التحديث

def update(frame):
    line.set_ydata(np.sin(x + frame / 10))
    return line,

يقوم np.sin(x + frame / 10) بتحريك الموجة الجيبية أفقيًا، مما يخلق تأثير الموجة المتحركة.

• إنشاء وعرض الرسوم المتحركة

ani = FuncAnimation(fig, update, frames=100, interval=50, blit=True)
plt.show()

وهذا يربط كل شيء معًا لإنشاء الرسوم المتحركة:

• fig: الشكل المراد تحريكه.
• update: الدالة التي يتم استدعاؤها لكل إطار.
• frames=100: عدد الإطارات في الرسوم المتحركة.
• interval=50: الفاصل الزمني بين الإطارات بالمللي ثانية (50 مللي ثانية = 20 إطارًا في الثانية).
• blit=True: يعمل على تحسين الأداء عن طريق إعادة رسم أجزاء الرسم البياني التي تتغير فقط.

• النتيجة

تحريك الفيزياء: الإطلاق المائل

سنوضح كيفية تحريك مثال كلاسيكي في دروس الفيزياء: الإطلاق المائل. سنتبع خطوات مشابهة للمثال الأساسي الموضح سابقًا.

• تحديد معلمات الحركة ومتجه الزمن

g = 9.81  # gravity (m/s^2)
v0 = 20   # initial velocity (m/s)
theta = np.radians(45)  # launch angle in radians

# total time the projectile will be in the air
t_flight = 2 * v0 * np.sin(theta) / g
# time vector with 100 equally spaced values between 0 and t_flight
t = np.linspace(0, t_flight, 100)

• حساب المسار

x = v0 * np.cos(theta) * t # horizontal position at time t
y = v0 * np.sin(theta) * t - 0.5 * g * t**2 # vertical position at time t

• إعداد الحبكة

fig, ax = plt.subplots()
ax.set_xlim(0, max(x)*1.1)
ax.set_ylim(0, max(y)*1.1)
ax.set_title("Oblique Launch")
ax.set_xlabel("Distance")
ax.set_ylabel("Height")
line, = ax.plot([], [], lw=2)
point, = ax.plot([], [], 'ro')  # red dot for projectile

• دالة التهيئة

في هذا المثال، سنستخدم دالة تهيئة لضبط كل شيء إلى حالة فارغة. وهي تُعيد عناصر الرسم البياني التي سيتم تحديثها أثناء الرسوم المتحركة.

def init():
    line.set_data([], [])
    point.set_data([], [])
    return line, point

• تحديث الدالة والرسوم المتحركة

def update(frame):
    line.set_data(x[:frame], y[:frame])     # trajectory up to current frame
    point.set_data(x[frame], y[frame])      # current projectile position
    return line, point

يتم استدعاء دالة التحديث في كل إطار. يشير مُعامل الإطار إلى مصفوفة الوقت، لذا فإن x[frame] و y[frame] يُعطيان الإحداثيات الحالية.

ani = FuncAnimation(fig, update, frames=len(t), init_func=init, blit=True, interval=30)

frames=len(t): إجمالي عدد خطوات الرسوم المتحركة.

interval=30: الوقت (بالمللي ثانية) بين الإطارات (~33 إطارًا في الثانية).

blit=True: يحسن الأداء عن طريق إعادة رسم أجزاء الإطار التي تغيرت فقط.

• النتيجة

تحريك الرياضيات: متسلسلات فورييه

في المثال التالي، سنوضح كيفية بناء موجة مربعة من دوال الجيب باستخدام تحويل فورييه.

• إنشاء قيم x ورسم بياني

x = np.linspace(-np.pi, np.pi, 1000)
y = np.zeros_like(x)
fig, ax = plt.subplots()
line, = ax.plot(x, y, lw=2)

# Setting text labels and axis limits
ax.set_title("Fourier Series Approximation of a Square Wave")
ax.set_ylim(-1.5, 1.5)
ax.set_xlim(-np.pi, np.pi)
text = ax.text(-np.pi, 1.3, '', fontsize=12)

x: مصفوفة من 1000 نقطة متباعدة بالتساوي من −π إلى π، وهو المجال النموذجي لسلسلة فورييه الدورية.

y: يقوم بتهيئة مصفوفة y من الأصفار، بنفس شكل x.

• تعريف دالة متسلسلة فورييه

الصيغة المستخدمة لمتسلسلة فورييه هي:

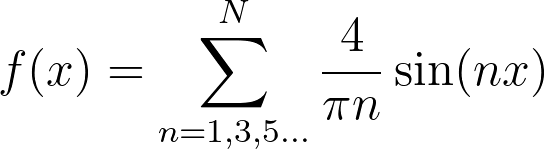
def fourier_series(n_terms):
    result = np.zeros_like(x)
    for n in range(1, n_terms * 2, 2):  # Only odd terms: 1, 3, 5, ...
        result += (4 / (np.pi * n)) * np.sin(n * x)
    return result

• ضبط دالة التحديث

def update(frame):
    y = fourier_series(frame + 1)
    line.set_ydata(y)
    text.set_text(f'{2*frame+1} terms')
    return line, text

تقوم هذه الدالة بتحديث الرسم البياني في كل إطار من الرسوم المتحركة:

• تحسب تقريبًا جديدًا باستخدامframe + 1 مصطلحات.
• تقوم بتحديث قيم y للخط.
• تقوم بتحديث التسمية لإظهار عدد المصطلحات المستخدمة (على سبيل المثال، “3 مصطلحات”، “5 مصطلحات”، إلخ).
• تعيد عناصر الرسم البياني المُحدَّثة لإعادة رسمها.

• إنشاء التصور

ani = FuncAnimation(fig, update, frames=20, interval=200, blit=True)
plt.show()

التعلم الآلي عملياً: انحدار التدرج

الآن، سنوضح كيف تجد خوارزمية التعلم الآلي الكلاسيكية الحد الأدنى على دالة مكافئة ثلاثية الأبعاد.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# Define the function and its gradient
def f(x, y):
    return x**2 + y**2

def grad_f(x, y):
    return 2*x, 2*y

# Initialize parameters
lr = 0.1
steps = 50
x, y = 4.0, 4.0  # start point
history = [(x, y)]

# Perform gradient descent
for _ in range(steps):
    dx, dy = grad_f(x, y)
    x -= lr * dx
    y -= lr * dy
    history.append((x, y))

# Extract coordinates
xs, ys = zip(*history)
zs = [f(xi, yi) for xi, yi in history]

# Prepare 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
X, Y = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
Z = f(X, Y)
ax.plot_surface(X, Y, Z, alpha=0.6, cmap='viridis')
point, = ax.plot([], [], [], 'ro', markersize=6)
line, = ax.plot([], [], [], 'r-', lw=1)

# Animation functions
def init():
    point.set_data([], [])
    point.set_3d_properties([])
    line.set_data([], [])
    line.set_3d_properties([])
    return point, line

def update(i):
    point.set_data(xs[i], ys[i])
    point.set_3d_properties(zs[i])
    line.set_data(xs[:i+1], ys[:i+1])
    line.set_3d_properties(zs[:i+1])
    return point, line

ani = FuncAnimation(fig, update, frames=len(xs), init_func=init, blit=True, interval=200)

• النتيجة

تصدير الرسوم المتحركة للويب والعروض التقديمية

وأخيرًا، لتصدير الرسوم البيانية المتحركة إلى ملف، يمكنك استخدام الدالة ()animation.save.

# Export as GIF (optional)
ani.save("launch.gif", writer='pillow', fps=30)

في المثال أعلاه، تأخذ الدالة كائن FuncAnimation، وتقوم بعرضه إطارًا تلو الآخر باستخدام مكتبة Pillow، وتصدر النتيجة كملف gif يسمى launch.gif بمعدل 30 إطارًا في الثانية.

في هذه المقالة، استعرضنا كيف يمكن لفئة الرسوم المتحركة من مكتبة matplotlib أن تكون مفيدة في توضيح آليات عمل الخوارزميات والعمليات الرياضية والفيزيائية. ويمكن توسيع نطاق الأمثلة التي تم استعراضها في هذه المقالة لإنشاء رسومات بيانية مؤثرة للمنشورات والمحاضرات والتقارير.

ولجعل هذه المقالة أكثر فائدة، أقترح استخدام الأمثلة المعروضة لإنشاء الرسوم المتحركة الخاصة بك ومحاكاة العمليات المتعلقة بمجالك.